Linked List Loop/Cycle Detection

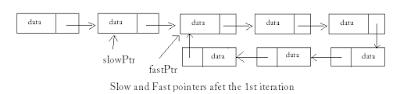
Problem: Given the head pointer to a singly linked list with a loop or cycle in it. If you were to walk this list you never arrive at the end or the tail of the linked list. Find whether the list contains a loop in O(n) time and space complexity. Observation: A linked list with a loop will have a node that is being pointed from 2 different node. Solution 1: This problem was solved in the late 1960s by Robert W. Floyd. The solution is aptly named as Floyd's cycle finding algorithm a.k.a the Tortoise and Hare algorithm. It uses 2 pointers moving at different speeds to walk the linked list. Once they enter the loop they are expected to meet, which denotes that there is a loop. This works because the only way a faster moving pointer would point to the same location as a slower moving pointer is if somehow the entire list or a part of it is circular. Think of a tortoise and a hare running on a track. The faster running hare will catch up with the tortoise if they are running on circular track instead of a straight strip. Code: //returns true if the linked list contains a loop

bool ListContainsLoop(Node * head)
{
Node * slowPtr = head;
Node * fastPtr = head;

while(slowPtr  && fastPtr)
{
 fastPtr = fastPtr->next; // advance the fast pointer
 if(fastPtr == slowPtr)   // and check if its equal to the slow pointer
     return true;         // loop detected

 if(fastPtr == NULL)
 {
     return false;        // since fastPtr is NULL we reached the tail
 }

 fastPtr = fastPtr->next; //advance and check again
 if(fastPtr == slowPtr)
     return true;

 slowPtr = slowPtr-next;  // advance the slow pointer only once
}
return false;                // we reach here if we reach the tail
}